El álgebra relacional consiste de algunas simples maneras de construir nuevas relaciones a partir de otras. Si pensamos que las relaciones iniciales son los datos almacenados, las nuevas relaciones se pueden ver como respuestas a algunas consultas deseadas.
Es un lenguaje de consulta procedural. Consta de un conjunto de operaciones que toman como entrada una o dos relaciones y producen como resultado una nueva relación, por lo tanto, es posible unir y combinar operadores. Hay ocho operadores en el álgebra relacional que construyen relaciones y manipulan datos.
5.1 OPERACIONES FUNDAMENTALES DEL ÁLGEBRA RELACIONAL
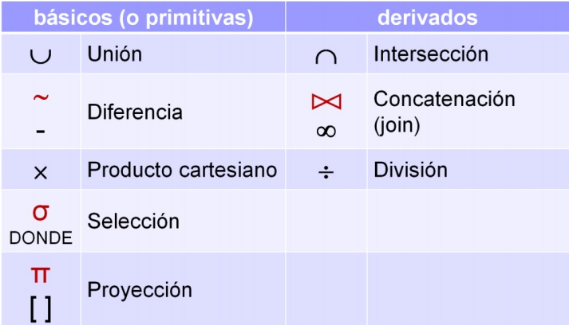
Ocho operadores, algunos de ellos son básicos o fundamentales y otros son derivados o forman parte de los operadores de extensión del álgebra relacional.
Selección
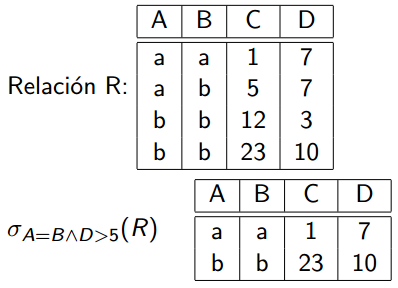
El operador de selección opta por tuplas que satisfagan cierto predicado, se utiliza la letra griega sigma minúscula (σ) para señalar la selección. El predicado aparece como subíndice de σ. La Relación que constituye el argumento se da entre paréntesis después de la σ. Utiliza operadores lógicos y matemáticos.
Formato: σ (condición) (R) Nombre de la Relación
EJEMPLO
Proyección
La operación de proyección permite quitar ciertos atributos de la relación, esta operación es unaria, copiando su relación base dada como argumento y quitando ciertas columnas, La proyección se señala con la letra griega pi mayúscula (Π). Como subíndice de Π se coloca una lista de todos los atributos que se desea aparezcan en el resultado. La relación argumento se escribe después de Π entre paréntesis.
Formato: π lista de atributos (R) Nombre de la Relación
EJEMPLO

Unión
Conjunto de todas las tuplas que pertenecen ya sea a A o a B o a Ambas. Al igual que en teoría de conjuntos el símbolo ∪ representa aquí la unión de dos relaciones.
Al adaptar los operadores de conjuntos a relaciones se debe asegurar que exista compatibilidad entre ellas.
- Tienen el mismo grado.
- Los atributos tienen el mismo nombre.
- El dominio del atributo-i de R es el mismo que el dominio del atributo-i en S, ∀i
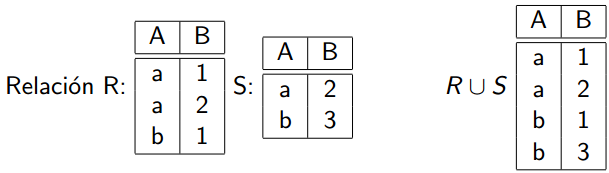
Formato: R ∪ S
EJEMPLO
Diferencia
Produce el conjunto de todas las tuplas t que pertenecen a A y no pertenecen a B, el simbolo utilizado es el clasio de la resta -.
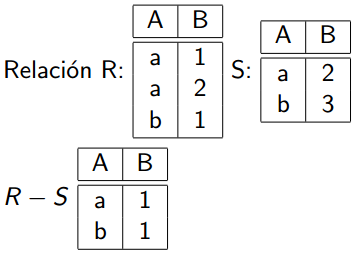
Formato: R - S
EJEMPLO
Producto cartesiano
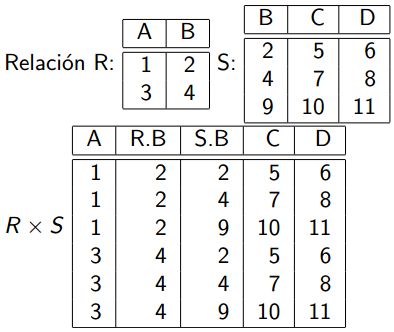
Produce el conjunto de todas las tuplas t tales que t es el encadenamiento de una tupla a perteneciente a A y de una b que pertenece a B. se utiliza el símbolo X para representar el producto. Si R y S tienen atributos en común se renombran. Para evitar ambigüedades se precede el nombre del atributo con el nombre de la relación.
Formato: R X S
EJEMPLO
Intersección
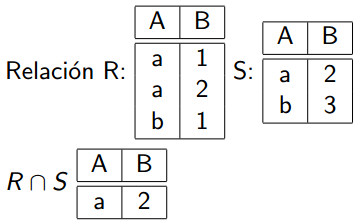
Produce el conjunto de todas las tuplas pertenecientes a A y B. Al igual que en teoría de conjuntos el símbolo ∩ representa aquí la intersección entre dos relaciones. Dentro del conjunto de operaciones en el álgebra relacional aparecen estas operaciones que no añaden potencia al algebra, pero simplifican las consultas habituales.
Cada operación re-emplaza un conjunto de operaciones “normales”.
- Intersección de conjuntos
- Reunión natural
- División
Formato: R ∩ S = R – (R – S)
EJEMPLO
Join
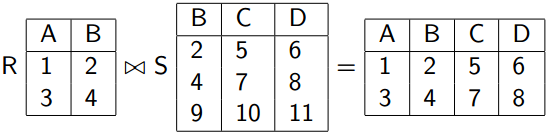
El JOIN Naturral es una operación binaria que permite combinar ciertas selecciones y un producto cartesiano en una sola operación. Se denota por el símbolo: ⋈
La reunión natural expresada en operaciones básicas equivale a:
R (X1;X2; … Xm; Y1;Y2; … ;Yn)
S (Y1;Y2; … ;Yn; Z1; Z2; … ; Zp)
Relación con atributos X, Y, Z y poblado por el conjunto de tuplas que tienen igual valor de Y en R y en S. π R U S (σ R.Y1=S.Y1 ^ R.Y2=S.Y2 ^...^ R.Yn=S.Yn (R X S))
EJEMPLO
Θ - Join
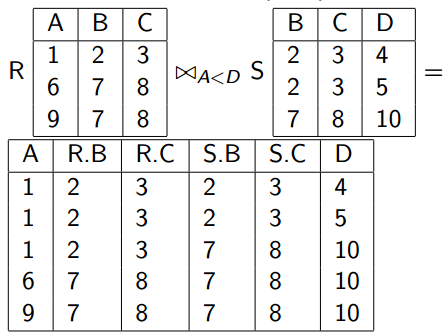
Equivalente al Join sólo que se permite usar cualquier condición de comparación. θ.
El resultado se construye:
- Toma el R X S
- Selecciona sólo las tuplas que satisfacen a θ.
Formato: R ⋈θ S
EJEMPLO
División
Sean R y S dos relaciones con esquemas:
(A1, ... ,An;B1, ... ,Bm) y (B1, ... , Bm) respectivamente.
La operación: (R ÷ S) da como resultado otra relación.
- cuyo esquema es (A1, … ,An)
- las tuplas tomadas a partir de las de r (R) tales que su valor (a1, … ,an) está asociado en r (R) con TODOS los valores (b1, … ,bm) que están en s (S)
Formato: (R ÷ S)
EJEMPLO

5.2 ÁLGEBRA RELACIONAL EXTENDIDA
1.- Una de las extensiones es permitir operaciones aritméticas como parte de la operación proyección (Proyección Generalizada).
2.- Permitir operaciones de agregación.
PROYECCIÓN GENERALIZADA
Amplía la proyección permitiendo que se utilicen funciones aritméticas en la lista de proyección. La operación proyección generalizada tiene la forma siguiente:
πF1, F2, ... ,Fn (E)
donde E es cualquier expresión del álgebra relacional y F1, F2, ... ,Fn son expresiones aritméticas que incluyen constantes y atributos pertenecientes al esquema E. Como caso especial la expresión aritmética puede ser simplemente un atributo o una constante. Cuando se hace uso de esta operación generalizada se recomienda dar nombre al atributo o columna generada con la función que se aplique.
Ejemplo: Suponga el esquema Tarjeta_credito (num-tarjeta, credito-disponible, limite-credito, vigencia, tipo) y se desea conocer lo gastado.
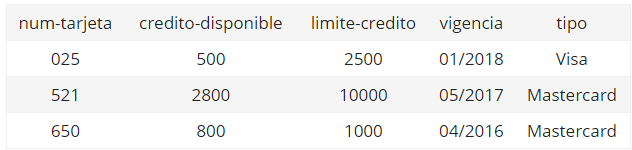
π num-tarjeta, (limite-credito - credito-disponible) AS credito-utilizado (Tarjeta_credito) la relación o esquema resultante sería a manera de ejemplo claro esta:

FUNCIONES DE AGREGACIÓN
Este tipo de operaciones se pueden como su nombre lo dice agregar a la operación de proyección, dichas operaciones toman un conjunto de valores y retornan o proyectan un valor ÚNICO. Las operaciones que veremos son:
-SUM: retorna la suma de los valores
-AVG: retorna la media de los valores
-MIN: retorna el mínimo de los valores
-MAX: retorna el máximo de los valores
-COUNT: retorna el número de elementos del conjunto
La forma general:
g1, g2…gn G f1(a1), f2(a2).. Fm(am)(E)
Donde:
g1,g2,…gn constituye la lista de atributos que indica como se realiza la agrupación.
fi es una función de agregación y ai es un nombre del atributo.
Considere el siguiente esquema Tarjeta-credito:
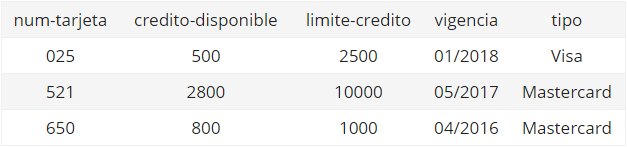
Ejemplo de SUM Supongamos que nos interesa conocer el total de credito que se otorga a todos los clientes. G sum(limite-credito) (Tarjeta-credito)

Conocer el total de los limites de créditos por tipo de tarjeta tendriamos lo siguiente: tipo G tipo, sum(limite-credito) AS total-credito-tipo (Tarjeta-credito)

Ejemplo de AVG Supongase que se desea calcular el promedio de los créditos disponibles. G avg(credito-disponible) (Tarjeta-credito)
Fuentes de información
Base de Datos 1 - Algebra Relacional
| Acerca de: |
|---|
| Éste es un sitio creado por estudiantes del Instituto Tecnológico de Pachuca, para la asignatura en curso; Fundamentos de Bases de Datos. |
| Equipo New Jackers: Hernández Salinas Lucio y Sanchez Casañas Jose María |
| Actividades Unidad 5 |